Truss (Docstrings)

This module can be used to solve problems related to 2D Trusses.

class sympy.physics.continuum_mechanics.truss.Truss

A Truss is an assembly of members such as beams, connected by nodes, that create a rigid structure. In engineering, a truss is a structure that consists of two-force members only.

Trusses are extremely important in engineering applications and can be seen in numerous real-world applications like bridges.

Examples

There is a Truss consisting of four nodes and five members connecting the nodes. A force P acts downward on the node D and there also exist pinned and roller joints on the nodes A and B respectively.

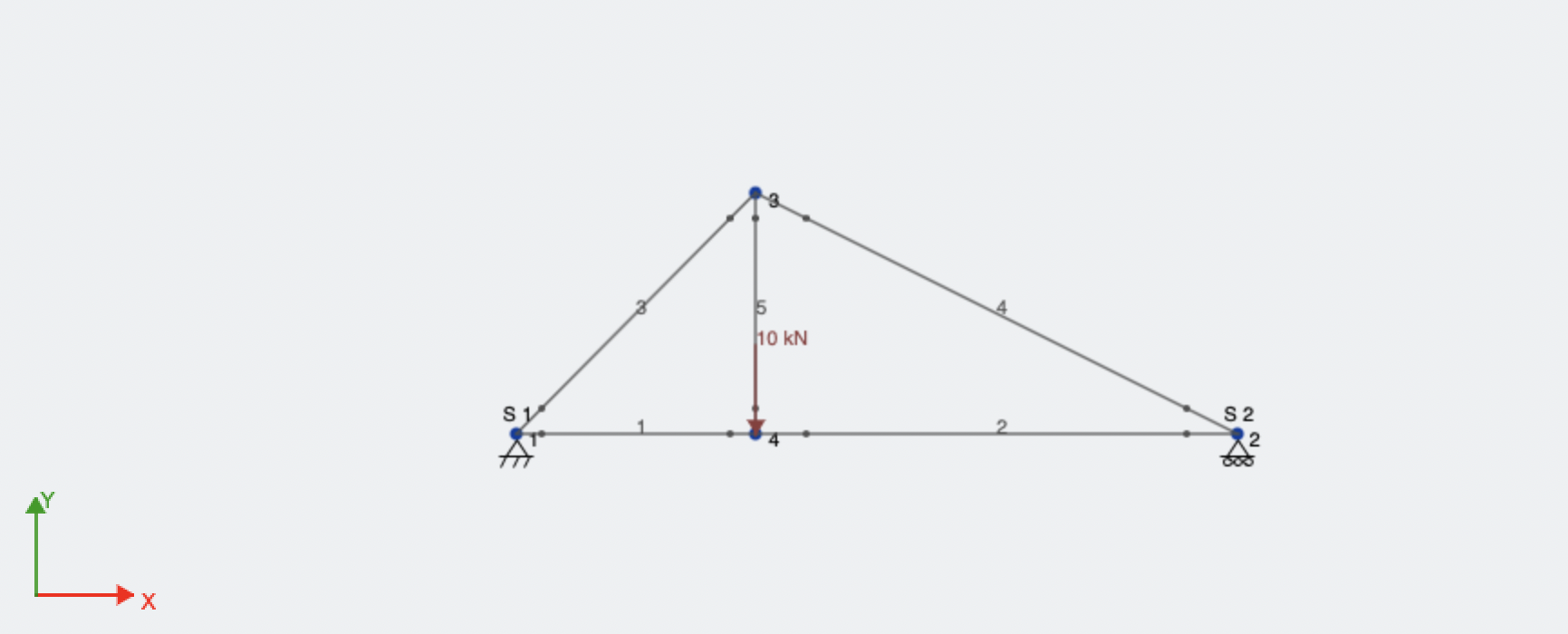
>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node("node_1", 0, 0)
>>> t.add_node("node_2", 6, 0)
>>> t.add_node("node_3", 2, 2)
>>> t.add_node("node_4", 2, 0)
>>> t.add_member("member_1", "node_1", "node_4")
>>> t.add_member("member_2", "node_2", "node_4")
>>> t.add_member("member_3", "node_1", "node_3")
>>> t.add_member("member_4", "node_2", "node_3")
>>> t.add_member("member_5", "node_3", "node_4")
>>> t.apply_load("node_4", magnitude=10, direction=270)
>>> t.apply_support("node_1", type="fixed")
>>> t.apply_support("node_2", type="roller")

add_member(label, start, end)

This method adds a member between any two nodes in the given truss.

Parameters:

label: String or Symbol

The label for a member. It is the only way to identify a particular member.

start: String or Symbol

The label of the starting point/node of the member.

end: String or Symbol

The label of the ending point/node of the member.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.add_node('C', 2, 2)
>>> t.add_member('AB', 'A', 'B')
>>> t.members
{'AB': ['A', 'B']}

add_node(label, x, y)

This method adds a node to the truss along with its name/label and its location.

Parameters:

label: String or a Symbol

The label for a node. It is the only way to identify a particular node.

x: Sympifyable

The x-coordinate of the position of the node.

y: Sympifyable

The y-coordinate of the position of the node.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.nodes
[('A', 0, 0)]
>>> t.add_node('B', 3, 0)
>>> t.nodes
[('A', 0, 0), ('B', 3, 0)]

apply_load(location, magnitude, direction)

This method applies an external load at a particular node

Parameters:

location: String or Symbol

Label of the Node at which load is applied.

magnitude: Sympifyable

Magnitude of the load applied. It must always be positive and any changes in the direction of the load are not reflected here.

direction: Sympifyable

The angle, in degrees, that the load vector makes with the horizontal in the counter-clockwise direction. It takes the values 0 to 360, inclusive.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> from sympy import symbols
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> P = symbols('P')
>>> t.apply_load('A', P, 90)
>>> t.apply_load('A', P/2, 45)
>>> t.apply_load('A', P/4, 90)
>>> t.loads
{'A': [[P, 90], [P/2, 45], [P/4, 90]]}

apply_support(location, type)

This method adds a pinned or roller support at a particular node

Parameters:

location: String or Symbol

Label of the Node at which support is added.

type: String

Type of the support being provided at the node.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.apply_support('A', 'pinned')
>>> t.supports
{'A': 'pinned'}

change_member_label(label, new_label)

This method changes the label of a member.

Parameters:

label: String or Symbol

The label of the member for which the label has to be changed.

new_label: String or Symbol

The new label of the member.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.nodes
[('A', 0, 0), ('B', 3, 0)]
>>> t.change_node_label('A', 'C')
>>> t.nodes
[('C', 0, 0), ('B', 3, 0)]
>>> t.add_member('BC', 'B', 'C')
>>> t.members
{'BC': ['B', 'C']}
>>> t.change_member_label('BC', 'BC_new')
>>> t.members
{'BC_new': ['B', 'C']}

change_node_label(label, new_label)

This method changes the label of a node.

Parameters:

label: String or Symbol

The label of the node for which the label has to be changed.

new_label: String or Symbol

The new label of the node.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.nodes
[('A', 0, 0), ('B', 3, 0)]
>>> t.change_node_label('A', 'C')
>>> t.nodes
[('C', 0, 0), ('B', 3, 0)]

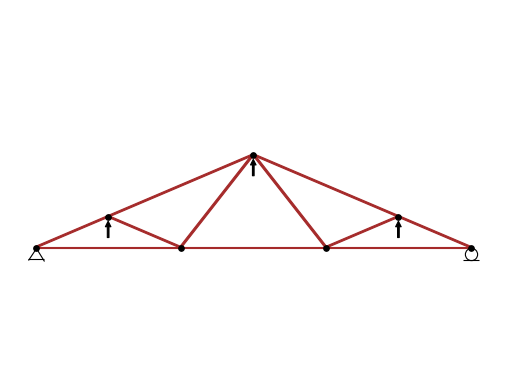
property internal_forces

Returns the internal forces for all members which are all initialized to 0.

property loads

Returns the loads acting on the truss.

property member_labels

Returns the members of the truss along with the start and end points.

property members

Returns the members of the truss along with the start and end points.

property node_labels

Returns the node labels of the truss.

property node_positions

Returns the positions of the nodes of the truss.

property nodes

Returns the nodes of the truss along with their positions.

property reaction_loads

Returns the reaction forces for all supports which are all initialized to 0.

remove_load(location, magnitude, direction)

This method removes an already present external load at a particular node

Parameters:

location: String or Symbol

Label of the Node at which load is applied and is to be removed.

magnitude: Sympifyable

Magnitude of the load applied.

direction: Sympifyable

The angle, in degrees, that the load vector makes with the horizontal in the counter-clockwise direction. It takes the values 0 to 360, inclusive.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> from sympy import symbols
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> P = symbols('P')
>>> t.apply_load('A', P, 90)
>>> t.apply_load('A', P/2, 45)
>>> t.apply_load('A', P/4, 90)
>>> t.loads
{'A': [[P, 90], [P/2, 45], [P/4, 90]]}
>>> t.remove_load('A', P/4, 90)
>>> t.loads
{'A': [[P, 90], [P/2, 45]]}

remove_member(label)

This method removes a member from the given truss.

Parameters:

label: String or Symbol

The label for the member to be removed.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.add_node('C', 2, 2)
>>> t.add_member('AB', 'A', 'B')
>>> t.add_member('AC', 'A', 'C')
>>> t.add_member('BC', 'B', 'C')
>>> t.members
{'AB': ['A', 'B'], 'AC': ['A', 'C'], 'BC': ['B', 'C']}
>>> t.remove_member('AC')
>>> t.members
{'AB': ['A', 'B'], 'BC': ['B', 'C']}

remove_node(label)

This method removes a node from the truss.

Parameters:

label: String or Symbol

The label of the node to be removed.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.nodes
[('A', 0, 0)]
>>> t.add_node('B', 3, 0)
>>> t.nodes
[('A', 0, 0), ('B', 3, 0)]
>>> t.remove_node('A')
>>> t.nodes
[('B', 3, 0)]

remove_support(location)

This method removes support from a particular node

Parameters:

location: String or Symbol

Label of the Node at which support is to be removed.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node('A', 0, 0)
>>> t.add_node('B', 3, 0)
>>> t.apply_support('A', 'pinned')
>>> t.supports
{'A': 'pinned'}
>>> t.remove_support('A')
>>> t.supports
{}

solve()

This method solves for all reaction forces of all supports and all internal forces of all the members in the truss, provided the Truss is solvable.

A Truss is solvable if the following condition is met,

2n >= r + m

Where n is the number of nodes, r is the number of reaction forces, where each pinned support has 2 reaction forces and each roller has 1, and m is the number of members.

The given condition is derived from the fact that a system of equations is solvable only when the number of variables is lesser than or equal to the number of equations. Equilibrium Equations in x and y directions give two equations per node giving 2n number equations. However, the truss needs to be stable as well and may be unstable if 2n > r + m. The number of variables is simply the sum of the number of reaction forces and member forces.

Note

The sign convention for the internal forces present in a member revolves around whether each force is compressive or tensile. While forming equations for each node, internal force due to a member on the node is assumed to be away from the node i.e. each force is assumed to be compressive by default. Hence, a positive value for an internal force implies the presence of compressive force in the member and a negative value implies a tensile force.

Examples

>>> from sympy.physics.continuum_mechanics.truss import Truss
>>> t = Truss()
>>> t.add_node("node_1", 0, 0)
>>> t.add_node("node_2", 6, 0)
>>> t.add_node("node_3", 2, 2)
>>> t.add_node("node_4", 2, 0)
>>> t.add_member("member_1", "node_1", "node_4")
>>> t.add_member("member_2", "node_2", "node_4")
>>> t.add_member("member_3", "node_1", "node_3")
>>> t.add_member("member_4", "node_2", "node_3")
>>> t.add_member("member_5", "node_3", "node_4")
>>> t.apply_load("node_4", magnitude=10, direction=270)
>>> t.apply_support("node_1", type="pinned")
>>> t.apply_support("node_2", type="roller")
>>> t.solve()
>>> t.reaction_loads
{'R_node_1_x': 0, 'R_node_1_y': 20/3, 'R_node_2_y': 10/3}
>>> t.internal_forces
{'member_1': 20/3, 'member_2': 20/3, 'member_3': -20*sqrt(2)/3, 'member_4': -10*sqrt(5)/3, 'member_5': 10}

property supports

Returns the nodes with provided supports along with the kind of support provided i.e. pinned or roller.